Lecture 9: Nonidentifiable models¶
(c) 2018 Justin Bois. With the exception of pasted graphics, where the source is noted, this work is licensed under a Creative Commons Attribution License CC-BY 4.0. All code contained herein is licensed under an MIT license.
This document was prepared at Caltech with financial support from the Donna and Benjamin M. Rosen Bioengineering Center.

This homework was generated from an Jupyter notebook. You can download the notebook here.
import numpy as np
import pandas as pd
import numba
import scipy.optimize
import scipy.stats as st
from statsmodels.tools import numdiff as smnd
import bebi103
import bokeh.io
import bokeh.plotting
bokeh.io.output_notebook()
A human immunodeficiency virus (HIV) is a virus that causes host organisms to develop a weaker, and sometimes ineffective, immune system. HIV inserts its viral RNA into a target cell of the immune system. This virus gets reverse transcribed into DNA and integrated into the host cell's chromosomes. The host cell will then transcribe the integrated DNA into mRNA for the production of viral proteins and produce new HIV. Newly created viruses then exit the cell by budding off from the host. HIV carries the danger of ongoing replication and cell infection without termination or immunological control. Because CD4 T cells, which communicate with other immune cells to activate responses to foreign pathogens, are the targets for viral infection and production, their infection leads to reductions in healthy CD4 T cell production, causing the immune system to weaken. This reduction in the immune response becomes particularly concerning after remaining infected for longer periods of time, leading to acquired immune deficiency syndrome (AIDS).
Perelson and coworkers have developed mathematical models to study HIV populations in the eukaryotic organisms. HIV-1 infects cells at a rate $k$ and is produced from these infected T cells at a rate $p$. On the other hand, the viruses are lost due to clearance by the immune system of drugs, which occurs at a rate $c$, and infected cells die at a rate $\delta$ (Figure from Perelson, Nat. Rev. Immunol., 2, 28-36, 2002)
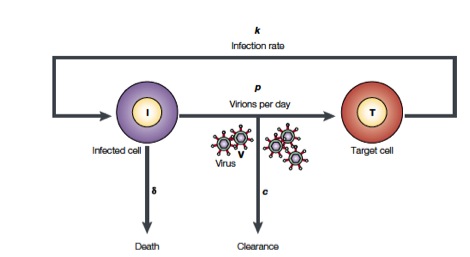
The above process can be written down as a system of differential equations.
\begin{align} \frac{dT^*}{dt} &= k V_I T - \delta T^*\\[1em] \frac{dV_I}{dt} &= -cV_I\\[1em] \frac{dV_{NI}}{dt} &= N \delta T^{*} - c V_{NI}, \end{align}
Here, $T(t)$ is the number of uninfected T-cells at time $t$, and $T^*$ is the number of infected T cells. Furthermore, there is a concentration $V_I(t)$ of infectious viruses that infect T cells at the rate $k$. We also have a concentration $V_{NI}$ of innocuous viruses. We define $N(t)$ to be the number of newly produced viruses from one infected cell over this cell's lifetime. We can measure the total viral load, $V(t) = V_I(t) + V_{NI}(t)$. If we initially have a viral load of $V(0) = V_0$, we can solve the system of differential equations to give
\begin{align} V(t;V_0,c,\delta) = V_0e^{-ct} + \frac{cV_0}{c-\delta}\left[\frac{c}{c-\delta}(e^{-{\delta}t} - e^{-ct}) - {\delta}te^{-ct}\right]. \end{align}
The data set¶
We will take viral load data from a real patient (which you can download here). The patient was treated with the drug Ritonavir, a protease inhibitor that serves to clear the viruses; i.e., it modulates $c$. So, in the context of the model, $c$ is a good parameter to use to understand the efficacy of a drug.
Let us take a quick look at the data set.
df = pd.read_csv('../data/hiv_data.csv', comment='#')
p = bokeh.plotting.figure(plot_height=250,
plot_width=450,
x_axis_label='days after drug administration',
y_axis_label='RNA copies per mL')
p.circle(df['Days after administration'], df['RNA copies per mL'])
bokeh.io.show(p)
After some noisy viral RNA levels early on, the virus begins to be cleared after about a day, bringing the viral load down.
Performing a curve fit to determine the parameters δ and c¶
The most common procedure to characterize the parameters δ and c is to minimize the sum of the square of the residuals between the theoretical equation given above and the measured data. As we showed in one of the homeworks, this is equivalent to finding the MAP parameter values for a model with a homoscedastic Gaussian likelihood and Uniform priors. Let's proceed to do this MAP calculation.
In the viral load model, we need to make sure that we don't get a divide by zero error when $c \approx \delta$. We will use the fact that
\begin{align} \lim_{c\to\delta} V(t;V_0,c,\delta) = V_0 \left(1 + \delta t + \frac{\delta^2 t^2}{2}\right)\mathrm{e}^{-\delta t}. \end{align}
We can now write our viral load model. Because we will be computing the posterior on a grid for plotting later, I am going to use Numba to speed things up.
@numba.jit(nopython=True)
def viral_load_model(p, t):
"""Perelman model for viral load"""
# Unpack parameters
V_0, c, delta = p
# If c and d are close, use limiting expression
if abs(c - delta) < 1e-9:
return V_0 * (1 + delta * t + (delta * t)**2 / 2) * np.exp(-delta * t)
# Proceed with typical calculation
bracket_term = ( c / (c - delta) * (np.exp(-delta * t) - np.exp(-c * t))
- delta * t * np.exp(-c * t) )
return V_0 * (np.exp(-c * t) + c / (c - delta) * bracket_term)
I will now code up the model. I will not use scipy.stats as we have been doing because I will later use the log posterior to make a plot, and I need fast calculations to make the plot of the marginalized posterior. In fact, to ease calculation, I will take the prior on the homoscedastic error $\sigma$ to be $g(\sigma) \propto 1/\sigma$. This enables marginalization of the posterior by hand. For this model, the posterior is
\begin{align} g(V_0, c, \delta, \sigma\mid \{t_i,V_i\}) \propto \frac{1}{\sigma^{N+1}}\exp\left[-\frac{1}{2\sigma^2}\sum_{i=1}^N(V_i-V(t_i;V_0,c, \delta))^2\right]. \end{align}
The integral to get the marginal posterior, where $\sigma$ is marginalized out, may be done analytically.
\begin{align} g(V_0, c, \delta \mid \{t_i,V_i\}) \propto \left(\sum_{i=1}^N(V_i-V(t_i;V_0,c, \delta))^2\right)^{-N/2}. \end{align}
We will then use this as out posterior.
@numba.jit(nopython=True)
def resid(p, t, V):
"""Residuals for viral load model with log parameters."""
return V - viral_load_model(p, t)
@numba.jit(nopython=True)
def log_prior(p, p_max):
"""Log prior; p_max is max allowed value of param, min is zero."""
if (p < 0).any() or (p > p_max).any():
return -np.inf
return 0.0
@numba.jit(nopython=True)
def log_likelihood(p, t, V):
"""Log likelihood for viral load model (Student-t distributed)."""
return -len(t) / 2 * np.log(np.sum(resid(p, t, V)**2))
@numba.jit(nopython=True)
def log_posterior(p, t, V, p_max):
"""Log posterior for viral load model."""
lp = log_prior(p, p_max)
if lp == -np.inf:
return -np.inf
return lp + log_likelihood(p, t, V)
@numba.jit(nopython=True)
def neg_log_posterior(p, t, V, p_max):
"""Negative log posterior for minimization purposes."""
return -log_posterior(p, t, V, p_max)
Based on the plot of the data, we will guess $V_0 \approx 150000$ RNA copies/mL. We'll guess that $c$ is dominating the drop in load and choose $c \approx 3$ days$^{-1}$. We'll guess $\delta$ is slower, say 0.3 day$^{-1}$. Now, we'll perform the curve fit and compute the covariance matrix to get error bars.
# Initial guess
p0 = np.array([150000, 3, 0.3])
# Max values
p_max = np.array([1e6, 50, 50])
# Find MAP
args = (df['Days after administration'].values,
df['RNA copies per mL'].values,
p_max)
res = scipy.optimize.minimize(neg_log_posterior, p0, args=args, method='powell')
popt = np.array(res.x, dtype=float)
# Approximate as Gaussian and compute covariance
cov = -np.linalg.inv(smnd.approx_hess(popt, log_posterior, args=args))
err_bars = np.sqrt(np.diag(cov))
# Print results to screen
print("""
V_0 = {0:.2e} ± {1:.2e} copies of RNA/mL
c = {2:.2f} ± {3:.2f} 1/days
δ = {4:.2f} ± {5:.2f} 1/days
""".format(popt[0], err_bars[0], popt[1], err_bars[1], popt[2], err_bars[2]))
Now, let's plot the regression line with the data.
# Plot the regression line
t_smooth = np.linspace(0, 7, 200)
p.line(t_smooth, viral_load_model(popt, t_smooth),
color='orange', line_width=2)
bokeh.io.show(p)
We have managed to find the MAP and give error bars based on the Gaussian approximation, and the curve seems to fit the data. Great! Now, for a sanity check, let's plot the posterior.
We want to make a contour plot in the $c$-$\delta$ plane, so we need to marginalize over $V_0$. We will do this numerically, using np.trapz().
# Values of c, delta, and V_0 to consider
c_plot = np.linspace(0.01, 10, 301)
delta_plot = np.linspace(0.01, 10, 300)
V_0_plot = np.linspace(6e4, 1.8e5, 99)
cc, dd, VV = np.meshgrid(c_plot, delta_plot, V_0_plot)
# Pull out data
t = df['Days after administration'].values
V = df['RNA copies per mL'].values
# Compute log of the posterior
@numba.jit(nopython=True)
def compute_log_post(c_plot, delta_plot, V_0_plot, cc, t, V, p_max):
log_post = np.empty_like(cc)
for j, c in enumerate(c_plot):
for i, d in enumerate(delta_plot):
for k, V_0 in enumerate(V_0_plot):
p = np.array([V_0, c, d])
log_post[i, j, k] = log_posterior(p, t, V, p_max)
return log_post - log_post.max()
# Compute log posterior
log_post = compute_log_post(c_plot, delta_plot, V_0_plot, cc, t, V, p_max)
# Marginalize
post_marg = np.trapz(np.exp(log_post), x=V_0_plot, axis=2)
Now that we have computed the marginalized posterior, we can plot it. I include the location of the MAP as found from optimization.
# Plot the contour
p = bebi103.viz.contour(cc[:,:,0],
dd[:,:,0],
post_marg,
overlaid=True,
line_width=0.5,
x_axis_label='c (1/days)',
y_axis_label='δ (1/days)')
p.cross(popt[1], popt[2], color='red', size=7)
bokeh.io.show(p)
Wow! The posterior has an odd shape; it is very far from Gaussian. The long, stretched contour implies that for a given low value of $\delta$, $c$ may take on a wide range of values. There is a maximum that the solver will find, we are unreasonably sure of its value. What we have is a nonidentifiable model.
A principled Bayesian approach would have caught this issue¶
If we instead took a principled Bayesian approach, the nonidentifiability the model would be more apparent. Let's proceed by taking such an approach. First, we need to define priors for the parameters. We do so noting that we divid the viral load by 100,000 to bring the measured quantities close to order unity. That is, we choose units for the viral load that is number of RNA molecules per 100 µL.
Because we have to choose a proper prior, we cannot sample exactly out of the distribution used in the naive regression. (Well, we could sample out of it, but we cannot do prior predictive checks.) So, we will choose a very broad prior for $c$ and $\delta$. So, here is our model.
\begin{align} &V_0 \sim \text{Norm}(1, 0.2),\\[1em] &c \sim \text{HalfNorm}(0, 500),\\[1em] &\delta \sim \text{HalfNorm}(0, 500), \\[1em] &\sigma_0 \sim \text{HalfNorm}(0, 0.2),\\[1em] & \sigma = \sigma_0\,V(t_i;V_o,c,\delta),\\[1em] &V_i \sim \text{Norm}(V(t_i;V_o,c,\delta), \sigma). \end{align}
We can now code up posterior predictive checks.
model_code_prior_pred = """
functions {
real V_theor(real t, real V0, real c, real delta) {
real return_value;
real bracketed_term;
if (fabs(c - delta) < 1e-9) {
return_value = 1 + delta * t + (delta * t)^2 / 2.0;
return_value *= V0 * exp(-delta * t);
}
else {
bracketed_term = c / (c - delta) * (exp(-delta * t) - exp(-c * t));
bracketed_term -= delta * t * exp(-c * t);
return_value = V0 * (exp(-c * t) + c / (c - delta) * bracketed_term);
}
return return_value;
}
}
data {
int N;
real t[N];
}
generated quantities {
real sigma[N];
real V_hat[N];
real V_ppc[N];
real V0 = normal_rng(1.0, 0.2);
real c = fabs(normal_rng(0.0, 500));
real delta = fabs(normal_rng(0.0, 500));
real sigma_0 = fabs(normal_rng(0.0, 0.2));
for (i in 1:N) {
V_hat[i] = V_theor(t[i], V0, c, delta);
sigma[i] = sigma_0 * V_hat[i];
V_ppc[i] = normal_rng(V_hat[i], sigma[i]);
}
}
"""
sm_prior_pred = bebi103.stan.StanModel(model_code=model_code_prior_pred)
Now we can draw out prior predictive check data sets.
data = {'N': len(df),
't': df['Days after administration'].values,
'V': df['RNA copies per mL'].values / 1e5}
samples_prior_pred = sm_prior_pred.sampling(data=data,
algorithm='Fixed_param',
iter=200,
warmup=0,
chains=1)
We can plot them to see how they look.
df_ppc = bebi103.stan.extract_array(samples_prior_pred, 'V_ppc')
p = bokeh.plotting.figure(plot_height=250,
plot_width=450,
x_axis_label='days after drug administration',
y_axis_label='RNA copies per 100 µL')
for _, g in df_ppc.groupby('chain_idx'):
p.line(t, g['V_ppc'], line_width=0.5, alpha=0.5)
bokeh.io.show(p)
Most prior predictive samples have a very fast clearance of RNA. This is because of the broad prior. We allow for very high values of $c$ and $\delta$. This immediately exposes a problem with choosing Uniform priors. They are actually very informative! They bias the data sets generated by the model toward incredibly fast clearange.
Nonetheless, we at least have the possibility of a slower clearance, so we wil proceed with this model. I'll code up the Stan model and then sample out of it.
model_code = """
functions {
real V_theor(real t, real V0, real c, real delta) {
real return_value;
real bracketed_term;
if (fabs(c - delta) < 1e-9) {
return_value = 1 + delta * t + (delta * t)^2 / 2.0;
return_value *= V0 * exp(-delta * t);
}
else {
bracketed_term = c / (c - delta) * (exp(-delta * t) - exp(-c * t));
bracketed_term -= delta * t * exp(-c * t);
return_value = V0 * (exp(-c * t) + c / (c - delta) * bracketed_term);
}
return return_value;
}
}
data {
int N;
real t[N];
real V[N];
}
parameters {
real V0;
real<lower=0> c;
real<lower=0> delta;
real<lower=0> sigma_0;
}
transformed parameters {
real V_hat[N];
real sigma[N];
for (i in 1:N) {
V_hat[i] = V_theor(t[i], V0, c, delta);
sigma[i] = sigma_0 * V_hat[i];
}
}
model {
V0 ~ normal(1, 0.2);
c ~ normal(0, 500);
delta ~ normal(0, 500);
sigma_0 ~ normal(0, 0.2);
V ~ normal(V_hat, sigma);
}
"""
sm = bebi103.stan.StanModel(model_code=model_code)
samples = sm.sampling(data=data)
bebi103.stan.check_all_diagnostics(samples)
Yikes! The diagnostics look pretty bad. Let's take a look at a parallel coordinate plot to see what is going on.
bokeh.io.show(bebi103.viz.parcoord_plot(samples, pars=['V0', 'c', 'delta', 'sigma_0']))
We see that when $c$ is high, $\delta$ is low, and vice versa. By zooming, we can see that the divergences are all associated with $\delta\approx 1/2$. Let's look at the corner plot to see if we can make out any other issues.
bokeh.io.show(bebi103.viz.corner(samples,
pars=['V0', 'c', 'delta', 'sigma_0'],
xtick_label_orientation='vertical'))
We see a similar structure as in our plot of the analytical expression for the posterior. We have very long tails on $c$ and $\delta$, a sure sign that the model is not identified. This nonidentification is probably what is causing our problems in the diagnostics. In order to make it identified, we need to have a more informative prior. Unfortunately, we do now know a priori what the relative magnitudes $c$ and $\delta$ are. Apparently, this is what the experiment is trying to ascertain.
Importantly, this analysis shows us that we need another experiment to nail down a prior on $\delta$ (or $c$) in order to have a model where we can get a good estimate of $c$ (or $\delta$). Importantly, if $\delta$ is about 0.5 days$^{-1}$ or less, $c$ remains unidentifiable. Unfortunately, the result from this paper is that δ ≈ 0.48 ± 0.4 days$^{-1}$. (I am a bit skeptical of this result, though, since the authors did not check whole posterior distributions and again used a MAP-based analysis to get this number in another experiment, this time in macaques.) If we use this as an informative prior, we still see a nonidentidiability in $c$, as we can see by sampling.
model_code = """
functions {
real V_theor(real t, real V0, real c, real delta) {
real return_value;
real bracketed_term;
if (fabs(c - delta) < 1e-9) {
return_value = 1 + delta * t + (delta * t)^2 / 2.0;
return_value *= V0 * exp(-delta * t);
}
else {
bracketed_term = c / (c - delta) * (exp(-delta * t) - exp(-c * t));
bracketed_term -= delta * t * exp(-c * t);
return_value = V0 * (exp(-c * t) + c / (c - delta) * bracketed_term);
}
return return_value;
}
}
data {
int N;
real t[N];
real V[N];
real delta_mu;
real delta_sigma;
}
parameters {
real V0;
real<lower=0> c;
real delta;
real<lower=0> sigma_0;
}
transformed parameters {
real V_hat[N];
real sigma[N];
for (i in 1:N) {
V_hat[i] = V_theor(t[i], V0, c, delta);
sigma[i] = sigma_0 * V_hat[i];
}
}
model {
V0 ~ normal(1, 0.2);
c ~ normal(0, 500);
delta ~ normal(delta_mu, delta_sigma);
sigma_0 ~ normal(0, 0.2);
V ~ normal(V_hat, sigma);
}
"""
sm = bebi103.stan.StanModel(model_code=model_code)
data['delta_mu'] = 0.48
data['delta_sigma'] = 0.04
samples = sm.sampling(data=data, control={'adapt_delta': 0.99})
bebi103.stan.check_all_diagnostics(samples)
Let's look at a corner plot.
bokeh.io.show(bebi103.viz.corner(samples,
pars=['V0', 'c', 'delta', 'sigma_0'],
xtick_label_orientation='vertical'))
The nonidentifiability of $c$ is clear.Most probability masee looks just like the prior. If, however, $\delta$ was big enough, we can identify $c$. Taking $\delta \approx 2 \pm 0.05$ days$^{-1}$, we can get a good marginal posterior for $c$.
data['delta_mu'] = 2.0
data['delta_sigma'] = 0.05
samples = sm.sampling(data=data, control={'adapt_delta': 0.99})
bebi103.stan.check_all_diagnostics(samples)
bokeh.io.show(bebi103.viz.corner(samples,
pars=['V0', 'c', 'delta', 'sigma_0'],
xtick_label_orientation='vertical'))
Conclusions¶
In summary, this analysis demonstrates that a principled modeling approach is crucial to be able to understand to any confidence what your parameter estimates really are. It also helps show what questions your experiment can and cannot answer. In this case, at best we can get a lower bound for $c$, but really have no idea how effective it is. And we would be completely ignorant that this is the case if we just naively used a MAP to do our parameter estimates.
Computing environment¶
%load_ext watermark
%watermark -v -p numpy,pandas,scipy,numba,statsmodels,pystan,bokeh,bebi103,jupyterlab