Solution

Data set download

---

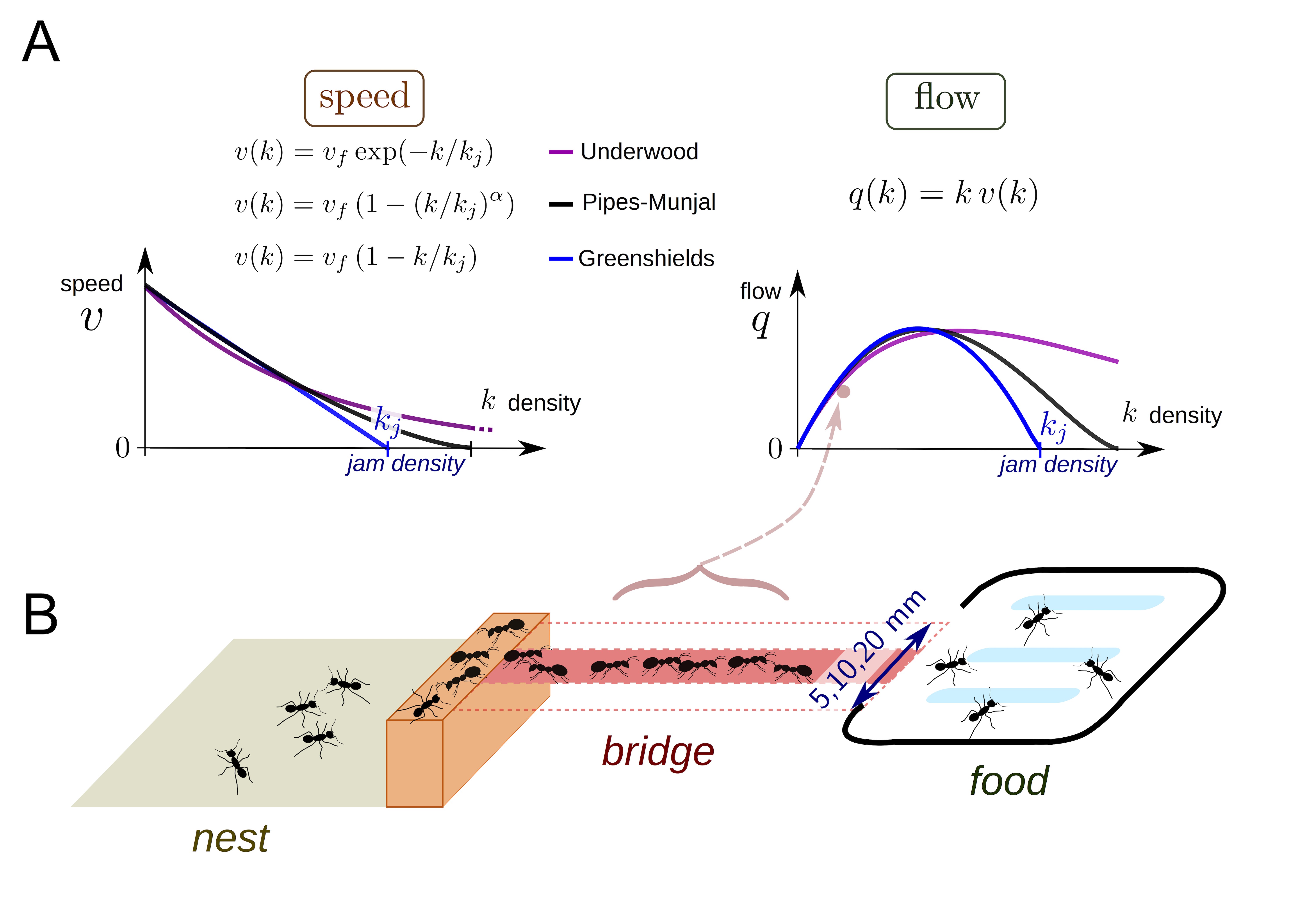
In collective behavior, individual interactors often look out only for their own immediate, short term interest within a crowd. This leads to issues like traffic jams on the road or in crowded pedestrian settings. In general, the flow (speed of moving objects times their density), often increases as density increases until hitting a critical point where the increased density gives rise to a traffic jam and flow begins to decrease. Poissonnier et al. were interested in how ants handle traffic. Unlike human pedestrians or drivers, ants may act more cooperatively in foraging to maximize food acquisition since they share a common goal of raising more young. Today, we will model traffic in ants and see whether they get into jams.

In order to look at ant collective behavior at different densities, the authors starved ant colonies of varying sizes for a few days, and then provided them a foraging object (sugar!) via a bridge of varying width (B). The ants would climb across the bridge to get to the sugar and then return to colony. The variable colony size and bridge width lead to different densities of foraging ants on the bridge, which the authors took (170!) videos of. They measured density and flow across the bridge from the videos. They were interested in how different older models of traffic jams from human behaviors (A) might fit their data and how this might inform whether ants get into traffic while trying to forage.

As this is an eLife paper, the data is (supposed to be) publicly available. There was an issue with the Dryad repository for the data (the DOI link was broken), but the corresponding author very promptly sent me the data when I emailed her. You can download the data set here. We will begin with some exploration for the data before building some models!

import numpy as np
import pandas as pd

import bebi103

import bokeh
import bokeh.io
import bokeh.util.hex
import bokeh_catplot

import cmdstanpy
import arviz as az

bokeh.io.output_notebook()

Loading BokehJS ...

We will read in the data and take a look at the format.

df = pd.read_csv("../data/ant_traffic.txt", delimiter="\t")
df.head()

	D	F
0	0.5	0.5
1	0.5	0.0
2	0.5	0.0
3	0.5	0.0
4	0.5	0.0

Here, 'D' represents ant density (in \(\mathrm{ant}/\mathrm{cm}^2\), based on the figure in the paper), ant 'F' indicates flow, which is \(\mathrm{ant}/\mathrm{cm}/\mathrm{s}\), also based on the figure. The authors generated a lot of data here (170 hour long videos sampled at 1 Hz \(\approx 600,000\) data points), so we might have a little trouble handling that much data with sampling. They use optimization to get their curve fits, which is a reasonable choice since they are data rich here. To speed things up for the sake of this exercise, I will thin the data stochastically. This shouldn’t influence the modeling much, and I did some testing and found only quite small differences for the samples of the parameters after thinning the data. We will take a look at the thinned data as compared to the full set to do another sanity check that we aren’t losing too much information. With this many data points, transparency doesn’t always capture the distribution of data points, since it caps out at fully opaque, so I also put a hexplot with a log colormap to get another idea for the data.

df_thin = df.sample(n=10000, random_state=24601)

p = bokeh.plotting.figure(
    frame_width=250,
    frame_height=250,
    x_axis_label="Density k (ant/cm^2)",
    y_axis_label="Flow q (ant/cm/s)",
    title="Thinned Data",
)

p.circle("D", "F", source=df_thin, alpha=0.05)


x, y, hex_size = df_thin["D"], df_thin["F"], 0.5

bins = bokeh.util.hex.hexbin(x, y, hex_size)

q = bokeh.plotting.figure(
    match_aspect=True,
    background_fill_color="#440154",
    frame_width=250,
    frame_height=250,
    x_axis_label="Density k (ant/cm^2)",
    y_axis_label="Flow q (ant/cm/s)",
)
q.grid.visible = False

q.hex_tile(
    q="q",
    r="r",
    size=hex_size,
    line_color=None,
    source=bins,
    fill_color=bokeh.transform.log_cmap("counts", "Viridis256", 0, max(bins.counts)),
)

color_bar = bokeh.models.ColorBar(
    color_mapper=bokeh.transform.log_cmap(
        "counts", "Viridis256", 0.0001, max(bins.counts)
    )["transform"],
    ticker=bokeh.models.LogTicker(),
    border_line_color=None,
    width=30,
    location=(0, 0),
    label_standoff=12,
)

q.add_layout(color_bar, "right")


s = bokeh.plotting.figure(
    frame_width=250,
    frame_height=250,
    x_axis_label="Density k (ant/cm^2)",
    y_axis_label="Flow q (ant/cm/s)",
    title="Full Data",
)

s.circle("D", "F", source=df, alpha=0.05)

x, y, hex_size = df["D"], df["F"], 0.5

bins = bokeh.util.hex.hexbin(x, y, hex_size)

r = bokeh.plotting.figure(
    match_aspect=True,
    background_fill_color="#440154",
    frame_width=250,
    frame_height=250,
    x_axis_label="Density k (ant/cm^2)",
    y_axis_label="Flow q (ant/cm/s)",
)
r.grid.visible = False

r.hex_tile(
    q="q",
    r="r",
    size=hex_size,
    line_color=None,
    source=bins,
    fill_color=bokeh.transform.log_cmap("counts", "Viridis256", 0, max(bins.counts)),
)

color_bar = bokeh.models.ColorBar(
    color_mapper=bokeh.transform.log_cmap(
        "counts", "Viridis256", 0.0001, max(bins.counts)
    )["transform"],
    ticker=bokeh.models.LogTicker(),
    border_line_color=None,
    width=30,
    location=(0, 0),
    label_standoff=12,
)

r.add_layout(color_bar, "right")

bokeh.io.show(bokeh.layouts.gridplot([p, q, s, r], ncols=2))

The thinning looks pretty reasonable. Keep in mind that the colormap is on a log scale, so the amount of weight that the far densities will get to influence the posterior is almost negligible compared to the densities below ~8. The authors also do a fit on the average of the flow at each density in order to increase the weight of the points on the high density portion of the graph. We can also plot that here. We use the full data set to get the mean.

df_mean = df.groupby("D").mean().reset_index()

p = bokeh.plotting.figure(
    frame_width=300,
    frame_height=300,
    x_axis_label="Density k (ant/cm^2)",
    y_axis_label="Mean flow q (ant/cm/s)",
)
p.circle("D", "F", source=df_mean, alpha=1)
bokeh.io.show(p)

It looks like the data is pretty linear in the early part of the regime, before the data becomes both much more sparse and may plateau. In order to try to get a model for ant traffic at these variable densities, the authors pulled several models from the literature. They start off with a parabolic shaped model (which makes sense for traffic, at some high density you start to get jammed up and are not able to increase flow, but instead it starts to reduce), an exponential, a modified parabola with an additional shape parameter \(\alpha\), and their own two-phase flow, which describes the data as a piecewise linear relationship with a linearly increasing portion which goes to a flat line at some density. Here are the mathematical models:

Greenshields:

\[q=k \cdot v_f \cdot \left( 1 - \frac{k}{k_j}\right)\]

Underwood:

\[q=k \cdot v_f \cdot \mathrm{e}^{\frac{-k}{k_j}}\]

Pipes-Munjal:

\[q=k \cdot v_f \cdot \left( 1 - \left(\frac{k}{k_j}\right)^\alpha\right)\]

Two-phase flow:

:nbsphinx-math:`begin{align}

q(k) = left{

begin{array}{lr}

k cdot v &mathrm{if} , k leq k_j\ k_j cdot v &mathrm{if} , k > k_j

end{array}

right.

end{align}`

For these equations, \(q\) is the flow, \(k\) is the density, \(k_j\) is the sort of threshold after which either jamming or plateauing of flow increase occurs, \(v_f\) is the free speed of interactors without contact, \(\alpha\) defines how fast the flow decays after threshold. With these in hand, we can begin to define a statistical model for our data generating process. This is where you come in! The best way to get comfortable modeling is to do it. Pick one or multiple mathematical models from above and construct a statistical model from it. Code that up in Stan and get samples! For your model, then fit the thinned data set and the averaged data set and make some comparisons of the results. For the sake of time, I have included code from Justin to plot the results once you write down your model and code it in Stan.

Model for Greenshields model:

\begin{align} &k_j \sim \text{Norm}(50, 10),\\[1em] &v_f \sim \text{Gamma}(3, 2),\\[1em] &\sigma \sim \text{HalfNorm}(0,1.0),\\[1em] &k_i \sim \text{Norm}(\text{greensheilds}(k_i, v_f, k_j), \sigma)\; \forall i. \end{align}

sm_prior_pred = cmdstanpy.CmdStanModel(
    stan_file="ant_traffic_prior_predictive.stan"
)

INFO:cmdstanpy:stan to c++ (/Users/bois/Dropbox/git/bebi103_course/2020/b/content/recitations/recitation_05/ant_traffic_prior_predictive.hpp)
INFO:cmdstanpy:compiling c++
INFO:cmdstanpy:compiled model file: /Users/bois/Dropbox/git/bebi103_course/2020/b/content/recitations/recitation_05/ant_traffic_prior_predictive

With the code ready for the prior predictive checks, you are ready to sample!

k = df_thin['D'].values

k = np.linspace(0, k.max(), 2000)

data = {
    "N": len(k),
    "k": k,
    "k_j_mu": 50.0,
    "k_j_sigma": 10.0,
    "v_f_alpha": 3.0,
    "v_f_beta": 2.0,
    "sigma_mu": 0.0,
    "sigma_sigma": 1.0,
    "alpha_alpha":3.0,
    "alpha_beta":2.0
}

samples = sm_prior_pred.sample(data=data, sampling_iters=1000, fixed_param=True)

INFO:cmdstanpy:start chain 1
INFO:cmdstanpy:finish chain 1

Now we parse the data for our plots.

samples_greensheilds = az.from_cmdstanpy(posterior=samples, prior=samples, prior_predictive=['q_greensheilds'])
samples_underwood = az.from_cmdstanpy(posterior=samples, prior=samples, prior_predictive=['q_underwood'])
samples_pipesmunjal = az.from_cmdstanpy(posterior=samples, prior=samples, prior_predictive=['q_pipesmunjal'])
samples_twophase = az.from_cmdstanpy(posterior=samples, prior=samples, prior_predictive=['q_twophase'])

We will use a predictive regression here to get a sense of how we did.

bokeh.io.show(
    bokeh.layouts.gridplot([
    bebi103.viz.predictive_regression(
        samples_greensheilds.prior_predictive['q_greensheilds'],
        samples_x=k,
        percentiles=[30, 60, 90, 99],
        x_axis_label='density',
        y_axis_label='flow rate',
        title='greensheilds'
    ),
        bebi103.viz.predictive_regression(
        samples_underwood.prior_predictive['q_underwood'],
        samples_x=k,
        percentiles=[30, 60, 90, 99],
        x_axis_label='density',
        y_axis_label='flow rate',
        title='underwood'
    ),
       bebi103.viz.predictive_regression(
        samples_pipesmunjal.prior_predictive['q_pipesmunjal'],
        samples_x=k,
        percentiles=[30, 60, 90, 99],
        x_axis_label='density',
        y_axis_label='flow rate',
        title='pipesmunjal'
    ),
        bebi103.viz.predictive_regression(
        samples_twophase.prior_predictive['q_twophase'],
        samples_x=k,
        percentiles=[30, 60, 90, 99],
        x_axis_label='density',
        y_axis_label='flow rate',
        title='twostep'
    )
    ], ncols = 2
    )
)

These plots look pretty good! There are some cases where the flow rate goes negative, particularly at low values. This indicates it would probably be a good idea to model \(\sigma\) about our mathematical distribution differently (maybe as a function of the density?) but we will continue with an assumption of homoscedasticity for now. The nice thing about building models from scratch like this is that we can add additional layers of complexity if we are not happy with model performance. We are ready for sampling! Using the building blocks that we coded for the prior predictive, we can code up our model in Stan, prepare a dictionary with the data, and draw samples.

k = df_thin['D'].values
q = df_thin['F'].values

#k = df_mean['D'].values
#q = df_mean['F'].values

N_ppc = 200
k_ppc = np.linspace(0, k.max(), N_ppc)
data = {
    "N": len(k),
    "k": k,
    "q": q,
    "N_ppc": N_ppc,
    "k_ppc": k_ppc,
}

This format of the data will work to feed into all our models. The real work now is to code these up in Stan! I will just include one example of the Stan code here, as the only difference between the models is to call a different function for the mathematical model (all functions are here). For the Pipes-Munjal model, you would have to uncomment the lines declaring the parameter \(\alpha\) and it’s prior.

functions {
  real greensheilds(real k_i, real k_j, real v_f) {
    real q = k_i*v_f*(1- (k_i/k_j) );
    return q;
  }

  real underwood(real k_i, real k_j, real v_f) {
    real q = k_i*v_f*2.7182818285^(-k_i/k_j);
    return q;
    }

  real twophase(real k_i, real k_j, real v_f) {
    if (k_i <= k_j) {
      return k_i*v_f;
    } else {
      return k_j*v_f;
    }
  }

  real pipesmunjal(real k_i, real k_j, real v_f, real alpha) {
    real q = k_i*v_f*(1- (k_i/k_j)^alpha);
    return q;
  }
}

data {
  int<lower=1> N;
  int N_ppc;
  real k[N];
  real q[N];
  real k_ppc[N_ppc];

}

parameters {
  real<lower=0> k_j;
  real<lower=0> v_f;
  real<lower=0> sigma;
  //real<lower=0> alpha;
}

transformed parameters {
  real mu[N];

  for (i in 1:N) {
    mu[i] = greensheilds(k[i], k_j, v_f);
  }
}

model {
  k_j ~ normal(50.0, 10.0);
  v_f ~ gamma(3.0, 2.0);
  sigma ~ normal(0.0, 1.0);
  //alpha ~ gamma(3.0, 2.0);

  q ~ normal(mu, sigma);
}


generated quantities {
  real q_ppc[N_ppc];

for (i in 1:N_ppc) {
    real mu_ppc = greensheilds(k_ppc[i], k_j, v_f);
    q_ppc[i] = normal_rng(mu_ppc, sigma);
  }
}

Let’s sample!

sm = cmdstanpy.CmdStanModel(stan_file='ant_traffic_model_greensheilds.stan')

samples = sm.sample(data=data, sampling_iters=1000, chains=4)

samples = az.from_cmdstanpy(posterior=samples, posterior_predictive=["q_ppc"])

INFO:cmdstanpy:stan to c++ (/Users/bois/Dropbox/git/bebi103_course/2020/b/content/recitations/recitation_05/ant_traffic_model_greensheilds.hpp)
INFO:cmdstanpy:compiling c++
INFO:cmdstanpy:compiled model file: /Users/bois/Dropbox/git/bebi103_course/2020/b/content/recitations/recitation_05/ant_traffic_model_greensheilds
INFO:cmdstanpy:start chain 1
INFO:cmdstanpy:start chain 2
INFO:cmdstanpy:finish chain 1
INFO:cmdstanpy:start chain 3
INFO:cmdstanpy:finish chain 2
INFO:cmdstanpy:start chain 4
INFO:cmdstanpy:finish chain 3
INFO:cmdstanpy:finish chain 4

For this model, we can now visualize the posterior with a corner plot!

bokeh.io.show(
    bebi103.viz.corner(
        samples, pars=["k_j", "v_f", "sigma"], xtick_label_orientation=np.pi / 4
    )
)

No divergences, so that’s good. Before I comment on the results, let’s take a look at the posterior predictive check data.

q_ppc = samples.posterior_predictive['q_ppc'].stack(
    {"sample": ("chain", "draw")}
).transpose("sample", "q_ppc_dim_0")

bokeh.io.show(
    bebi103.viz.predictive_regression(
        q_ppc,
        samples_x=k_ppc,
        percentiles=[30, 50, 70, 99],
        data=np.vstack((k, q)).transpose(),
        x_axis_label='ant density, k [ant/cm^2]',
        y_axis_label='ant flow, q [ant/cm/s]',
        x_range=[0, k.max()],
    )
)

To be on the safe side, we should also take a look at the parallel coordinate plot.

bokeh.io.show(
    bebi103.viz.parcoord_plot(
        samples,
        transformation="minmax",
        pars=["k_j", "v_f", "sigma"],
    )
)

Looks good! Nothing looks out of the ordinary here. Now for some commentary on this model. Here, we are looking at the Greensheilds model. For one, it seems like a very simplistic model for this data: an uside down U shape (parabola). The data doesn’t really capture the downward part of the function, and doesn’t very convincingly enter the parabola peak regime either. This leads to a shape the is slightly curved, but mostly linear in the region with lots of data. Since almost all the data points fall in the regime of low-medium density, the full dataset pushes the model to prioritize fit in that regime. As a generative model this seems like a pretty pathological failure. Also, note that the parameter estimate is exceedingly high indeed for \(k_f\). This variable represents the peak of the parabola, where increased density begins to lead to a traffic jam, and hence reduced flow overall. Thinking about the number given here, around 95 ants per square centimeter, this is evidently problematic. The ants used in this study are large enough that They would probably have to start stacking on top of each other to reach density, which would certainly change the paradigm. The largest densities seen experimentally were ~18 ants per square centimeter. Take a look at what these high ant densities looked like on the bridge: here. Based on the video, a 4-5 times increase in the number of ants seems improbable. Also note that this puts the parameter estimate at ~\(5\) standard deviations away from the prior mean that we set. Even with \(10,000\) data points, this will influence the parameter, maybe dramatically. Looking at the curve fits from the paper, they place the \(k_j\) value for this parameter at ~\(200\). This is an order of magnitude higher than any measured density! This is a case where the choice of prior actually hugely influenced the inference. In this case, it is largely because the model fairly catastrophically fails to explain the data. Thinking about the parameter estimates, though, in the case of this model (as bad as it is) the prior effecting the outcome strikes me as a philosophically good thing in this case: we know that the jamming density of the ants can’t be extremely high simply given physical constraints of how many can pack into a given area. Also, video from above would be difficult to use to parse a situation where the ant density was also given by ants stacked on top of each other. If this model is an accurate representation of the generative process for the data, the data we have does not provide enough information to resolve this parameter.

We will now take a look at what happens if we fit the averaged data with the same model.

k = df_mean['D'].values
q = df_mean['F'].values

N_ppc = 200
k_ppc = np.linspace(0, k.max(), N_ppc)
data = {
    "N": len(k),
    "k": k,
    "q": q,
    "N_ppc": N_ppc,
    "k_ppc": k_ppc,
}

sm = cmdstanpy.CmdStanModel(stan_file='ant_traffic_model_greensheilds.stan')

samples = sm.sample(data=data, sampling_iters=1000, chains=4)

samples = az.from_cmdstanpy(posterior=samples, posterior_predictive=["q_ppc"])

bokeh.io.show(
    bebi103.viz.corner(
        samples, pars=["k_j", "v_f", "sigma"], xtick_label_orientation=np.pi / 4
    )
)

INFO:cmdstanpy:found newer exe file, not recompiling
INFO:cmdstanpy:compiled model file: /Users/bois/Dropbox/git/bebi103_course/2020/b/content/recitations/recitation_05/ant_traffic_model_greensheilds
INFO:cmdstanpy:start chain 1
INFO:cmdstanpy:start chain 2
INFO:cmdstanpy:finish chain 1
INFO:cmdstanpy:start chain 3
INFO:cmdstanpy:finish chain 2
INFO:cmdstanpy:start chain 4
INFO:cmdstanpy:finish chain 3
INFO:cmdstanpy:finish chain 4

These parameter estimates look totally different! \(v_f\) is pretty similar, which is a good sign, and makes sense for an ant: ~ 1-2 cm per second as max speed. This is also consistent with the value reported from a different experiment for speed of an ant alone on a bridge. Good on that front! For \(k_j\), the value given here is very different. Using the averaging approach much more heavily weighs the large data points, which results in model seeming to resolve this parameter, i.e. it indicates that we have sufficient information to see the jam density for the ants. However, the model then rather badly overshoots the early parts of the data, and undershoots in the center of the graph. The issue here is that the weighting leads to a model that explains much less of the data, though captures the upper points better (see posterior predictive below). This is a potential bias for the fit. However, this model is evidently a pretty bad one for this data, so much of the pathology is due to that mismatch.

q_ppc = samples.posterior_predictive['q_ppc'].stack(
    {"sample": ("chain", "draw")}
).transpose("sample", "q_ppc_dim_0")

bokeh.io.show(
    bebi103.viz.predictive_regression(
        q_ppc,
        samples_x=k_ppc,
        percentiles=[30, 50, 70, 99],
        data=np.vstack((k, q)).transpose(),
        x_axis_label='ant density, k [ant/cm^2]',
        y_axis_label='ant flow, q [ant/cm/s]',
        x_range=[0, k.max()],
    )
)

Building the other models will also give an idea of what is going on with the data, and what underlying generative process is at play. Soon, we will go into model selection, which will give a principled way of calling which model performs best to capture our data with the fewest needed parameters.

Computing environment

%load_ext watermark
%watermark -v -p numpy,pandas,cmdstanpy,arviz,bokeh,bebi103,jupyterlab

CPython 3.7.6
IPython 7.12.0

numpy 1.18.1
pandas 0.24.2
cmdstanpy 0.8.0
arviz 0.6.1
bokeh 1.4.0
bebi103 0.0.50
jupyterlab 1.2.6