Homework 4.2: MCMC with Boolean data (40 pts)

---

In this problem, we will work with data of the True/False type. Lots of data sets in the biological sciences are like this. For example, we might look at a certain mutation in Drosophila that affects development and we might check whether or not eggs hatch.

The data we will use comes from an experiment we have done in past years in Bi 1x here at Caltech. The experiment was developed by Meaghan Sullivan with help from Ravi Nath. Jimmy Hamilton and Sophie Walton also worked to improve the experiment. We studied a neural circuit in C. elegans using optogenetics.

A neural circuit is a series of interconnected neurons that create a pathway to transmit a signal from where it is received to where it causes a behavioral response in an animal. An example is the neural circuit involved in reversals in C. elegans. This circuit consists of three types of neurons: sensory neurons receive stimuli from the environment, command interneurons integrate information from many sensory neurons and pass a signal to the motor neurons, and motor neurons that control worm behavior, such as reversals.

There are six non-motor neurons acting in a circuit that responds to environmental cues and triggers a reversal, a shown in the figure below (based on Schultheis et. al. 2011). These include four sensory neurons (ALM, AVM, ASH, and PLM) and two interneurons (AVD and AVA). Each sensory neuron is sensitive to a different type of stimulus. For example, the sensory neuron we are studying (ASH) is sensitive to chemosensory stimuli such as toxins, while another neuron (PLM) is sensitive to mechanical stimuli (touch) in the posterior part of the worm’s body. The sensory neurons send signals that are integrated by the two command interneurons (AVA and AVD). Each sensory neuron can provide an impulse to the command interneurons at any time. In order for the command interneuron to fire and activate motor neurons, the sum of the stimuli at any point in time must exceed a certain threshold. Once the stimuli from one or more sensory neurons has induced an action potential in a command interneuron, that signal is passed to motor neurons which will modulate worm behavior.

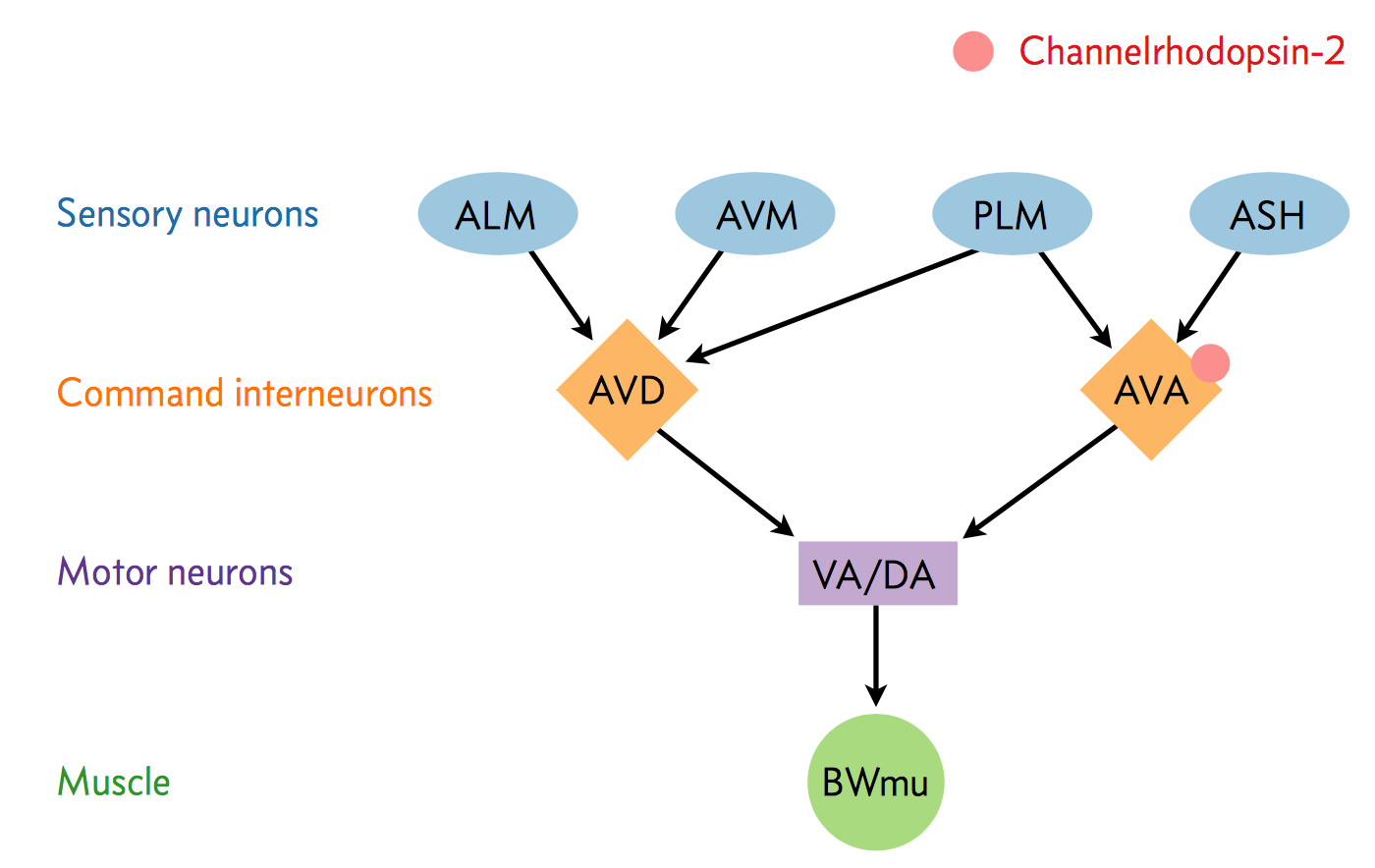
In the experiment, we used optogenetics to dissect the function of individual neurons in this circuit. We worked with two optogenetic worm strains. The ASH strain has Channelrhodopsin (ChR2, represented by a red barrel in the figure above) expressed only in the ASH sensory neuron. When we shine blue light on this strain, we should activate the ChR2, which will allow sodium and calcium cations to flow into the neuron, simulating an action potential. We want to quantify how robustly this stimulation will cause the worm to exhibit aversion behavior and reverse.

We also studied an AVA strain that has channelrhodopsin expressed only in the AVA command interneuron. Our goal is to quantify the effects of stimulating this neuron in terms of reversals compared to the ASH neuron and to wild type.

The True/False data here are the whether or not the worms undergo a reversal. Here is what the students observed.

Strain	Year	Trials	Reversals
WT	2017	55	7
ASH	2017	54	18
AVA	2017	52	28
WT	2016	36	6
ASH	2016	35	12
AVA	2016	36	30
WT	2015	35	0
ASH	2015	35	9
AVA	2015	36	33

For the purposes of this problem, assume that we can pool the results from the three years to have 13/126 reversals for wild type, 39/124 reversals for ASH, and 91/124 reversals for AVA.

Our goal is to estimate \(\theta\), the probability of reversal upon exposure to blue light for each strain. That is to say, we want to compute \(g(\theta\mid n, N)\), where \(n\) is the number of reversals in \(N\) trials.

a) Use Stan to get samples of \(\theta\) for each of the three strains. Plot either histograms or ECDFs of your samples.

b) Use your Metropolis-Hastings sampler from the previous problem to do the same.

c) The posterior plots of \(\theta\) are illuminating, but suppose we want to quantify the difference in reversal probability between the two strains, say strain 1 and strain 2. That is, we want to compute \(g(\delta_{12}\mid n_1, N_1, n_2, N_2)\), where \(\delta_{12} \equiv \theta_2 - \theta_1\). Note that computing this distribution by hand is quite difficult.