Display of MCMC samples¶

Data set download

[1]:

# Colab setup ------------------
import os, sys, subprocess
if "google.colab" in sys.modules:
    cmd = "pip install --upgrade iqplot colorcet bebi103 arviz cmdstanpy watermark"
    process = subprocess.Popen(cmd.split(), stdout=subprocess.PIPE, stderr=subprocess.PIPE)
    stdout, stderr = process.communicate()
    import cmdstanpy; cmdstanpy.install_cmdstan()
    data_path = "https://s3.amazonaws.com/bebi103.caltech.edu/data/"
else:
    data_path = "../data/"
# ------------------------------

import numpy as np
import pandas as pd

import cmdstanpy
import arviz as az

import iqplot
import bebi103

import holoviews as hv
hv.extension('bokeh')
bebi103.hv.set_defaults()

import bokeh.io
bokeh.io.output_notebook()

Loading BokehJS ...

In a previous lesson, we learned how to use Stan to sample out of posterior distributions specified by a generative model. In this lecture, we will learn about some techniques to visualize the results. As our first working example, we will consider again the conserved tubulin spindle size model, discussed at length previously, using the data set from Good, et al., Science, 342, 856-860, 2013.

We is a quick look at the data set.

[2]:

df = pd.read_csv(os.path.join(data_path, 'good_invitro_droplet_data.csv'), comment='#')

hv.Scatter(
    data=df,
    kdims='Droplet Diameter (um)',
    vdims='Spindle Length (um)',
)

Data type cannot be displayed:

[2]:

Visualization with ArviZ¶

ArviZ has lots of handy visualization of MCMC results, and it is a very promising package to use to quickly get plots. It currently still has some drawbacks. First, some plots are not rendered properly with Bokeh. This problem will likely be fixed very soon with future releases. Second, some of the aesthetic choices in the plots would not be my first choice. There are other specific drawbacks to the ArviZ visualizations that I will point out as we go along.

For each of the visualizations below, I show how to construct the visualization using ArviZ, but also using the bebi103 package.

Examining traces¶

The first type of visualization we will explore is useful for diagnosing potential problems with the sampler.

Trace plots¶

Trace plots are a common way of visualizing the trajectory a sampler takes through parameter space. We plot the value of the parameter versus step number. You can make these plots using bebi103.viz.trace_plot(). By default, the traces are colored according to chain number. In our sampling we just did, we used Stan’s default of four chains.

Trace plots with ArviZ¶

To make plots with ArviZ, the basic syntax is az.plot_***(samples, backend='bokeh'), where *** is the kind of plot you want. The backend="bokeh" kwarg indicates that you want the plot rendered with Bokeh. Let’s make a trace plot.

[5]:

az.plot_trace(samples, backend="bokeh");

ArviZ generates two plots for each variable. The plots to the right show the trace of the sampler. In this plot, the x-axis is the iteration number of the steps of the walker and the y-axis is the values of the parameter for that step.

ArviZ also plots a picture of the marginalized posterior distribution for each trace to the left. The issue I have these plots because they use kernel density estimation for the posterior plot. KDE involves selecting a bandwidth, which leaves an adjustable parameter. I prefer simply to plot the ECDFs of the samples to visualize the marginal distributions, as I show below.

Trace plots with bebi103¶

To make trace plots with the bebi103 module, you can do the following.

[6]:

bokeh.io.show(
    bebi103.viz.trace(samples)
)

Interpetation of trace plots¶

These trace plots look pretty good; the sampler is bounding around a central value. Trace plots are very commonly used, which is why I present them here, but are not particularly useful. This is not just my opinion. Here is what Dan Simpson has to say about trace plots.

Parallel coordinate plots¶

As Dan Simpson pointed out in his talk I linked to above, plots that visualize diagnostics effectively are better. We will talk more about diagnostics of MCMC in later lessons, but for now, I will display one of the diagnostic plots Dan showed in his talk. Here, we put the parameter names on the x-axis, and we plot the values of the parameters on the y-axis. Each line in the plot represents a single sample of the set of parameters.

Parallel coordinate plots with ArviZ¶

[7]:

az.plot_parallel(samples, backend='bokeh');

To make sure we compare things of the same magnitude so we can better see the details of how the parameters vary with respect to each other, we scale the samples by the minimum and maximum values.

[8]:

az.plot_parallel(
    samples, var_names=["phi", "gamma_", "sigma"], backend="bokeh", norm_method="minmax"
);

Parallel coordinate plots with bebi103¶

[9]:

bokeh.io.show(
    bebi103.viz.parcoord(
        samples,
        transformation="minmax",
        parameters=["phi", "gamma_", "sigma"],
    )
)

Intepretation of parallel coordinate plots¶

Normally, samples with problems are plotted in another color to help diagnose the problems. In this particular set of samples, there were no problems, so everything looks fine.

Interestingly, the “neck” between phi and gamma_ is indicative of anticorrelation. When φ is high, γ is low, and vice-versa.

Plots of marginalized distributions¶

While we cannot in general plot a multidimensional distribution, we can plot marginalized distributions, either of one parameter or of two.

Plotting marginalized distributions of one parameter¶

There are three main options for plotting marginalized distributions of a single parameter.

A kernel density estimate of the marginalized posterior.
A histogram of the marginalized posterior.
An ECDF of the samples out of the posterior for a particular parameter. This approximates the CDF of the marginalized distribution.

I prefer (3), though (2) is a good option as well. For continuous parameters, ArviZ offers only a KDE plot.

Plotting marginalized distributions with ArviZ¶

We already saw that ArviZ can give these plots along with trace plots. We can also directly plot them using the az.plot_density(). When using this function, the distributions are truncated at the bound of the highest probability density region, or HPD. If we’re considering a 95% credible interval, the HPD interval is the shortest interval that contains 95% of the probability of the posterior. By default, az.plot_density() truncates the plot of the KDE of the PDF for a 94% HPD.

[10]:

az.plot_density(samples, backend='bokeh');

Plotting marginalized distributions with iqplot¶

To get samples out of the marginalized posterior for a single parameter, we simply ignore the values of the parameters that are not the one of interest. We can then use iqplot to make plots of histograms or ECDFs.

To do so, we need to convert the posterior samples to a tidy data frame.

[11]:

# Convert to data frame
df_mcmc = bebi103.stan.arviz_to_dataframe(samples)

# Take a look
df_mcmc.head()

[11]:

	log10_phi	gamma_	sigma	phi	draw__	diverging__
0	1.57633	0.894319	3.69845	37.6987	0	False
1	1.57491	0.897639	3.70376	37.5758	1	False
2	1.58390	0.884862	3.85035	38.3623	2	False
3	1.58353	0.884912	3.84393	38.3288	3	False
4	1.58195	0.858369	3.58953	38.1898	4	False

Now, we can use iqplot to make histograms.

[12]:

hists = [
    iqplot.histogram(
        df_mcmc, q=param, density=True, rug=False, frame_height=150
    )
    for param in ["phi", "gamma_", "sigma"]
]

bokeh.io.show(bokeh.layouts.gridplot(hists, ncols=1))

A better option, in my opinion, is to make ECDFs of the samples.

[13]:

ecdfs = [
    iqplot.ecdf(
        df_mcmc, q=param, style="staircase", frame_height=150
    )
    for param in ["phi", "gamma_", "sigma"]
]

bokeh.io.show(bokeh.layouts.gridplot(ecdfs, ncols=1))

Marginal posteriors of two parameters¶

We can also plot the two-dimensional distribution (of most interest here are the parameters \(\phi\) and \(\gamma\)). The simplest way to plot these is simple to plot each point, possibily with some transparency.

[14]:

hv.Points(
    df_mcmc,
    kdims=[('phi', 'ϕ [µm]'), ('gamma_', 'γ')],
).opts(
    alpha = 0.1,
    size=2,
)

Data type cannot be displayed:

[14]:

Pair plots with ArviZ¶

We might like to do this for all pairs of plots. ArviZ enables this to be done conveniently.

[15]:

az.plot_pair(
    samples, var_names=["phi", "gamma_", "sigma"], backend="bokeh", figsize=(8, 8)
);

ArviZ also offers pair two-dimensional binning in the form of a hex plot. (This does not work properly with a Bokeh backend, so we use a Matplotlib backend.)

[16]:

az.plot_pair(
    samples,
    var_names=["phi", "gamma_", "sigma"],
    kind="hexbin",
    backend="matplotlib",
    figsize=(8, 8),
);

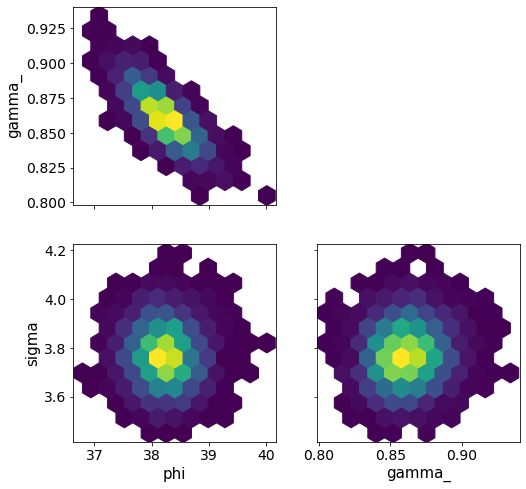
../../_images/lessons_12_display_of_mcmc_samples_40_0.png

Corner plots¶

It would be convenient to plot all visualizable marginal distributions (that is one- and two-dimensional distribution). We can conveniently do that with a corner plot, implemented in the bebi103 package.

[17]:

bokeh.io.show(
    bebi103.viz.corner(
        samples,
        parameters=[("phi", "ϕ [µm]"), ("gamma_", "γ"), ("sigma", "σ [µm]")],
        xtick_label_orientation=np.pi / 4,
    )
)

This is a nice way to summarize the posterior and is useful for visualizing how various parameters covary. We can also do a corner plot with the one-parameter marginalized posteriors represented as CDFs.

[18]:

bokeh.io.show(
    bebi103.viz.corner(
        samples,
        parameters=[("phi", "ϕ [µm]"), ("gamma_", "γ"), ("sigma", "σ [µm]")],
        plot_ecdf=True,
        xtick_label_orientation=np.pi / 4,
    )
)

In my view, this last plot is my preferred method of displaying results. All possible display-able marginal posteriors are plotted and laid out in a logical way.

[19]:

bebi103.stan.clean_cmdstan()

Computing environment¶

[20]:

%load_ext watermark
%watermark -v -p numpy,pandas,cmdstanpy,arviz,bokeh,holoviews,iqplot,bebi103,jupyterlab
print("cmdstan   :", bebi103.stan.cmdstan_version())

CPython 3.8.5
IPython 7.19.0

numpy 1.19.2
pandas 1.2.1
cmdstanpy 0.9.67
arviz 0.11.0
bokeh 2.2.3
holoviews 1.14.0
iqplot 0.2.0
bebi103 0.1.2
jupyterlab 2.2.6
cmdstan   : 2.26.0

Display of MCMC samples¶

Visualization with ArviZ¶

The model and samples¶

Examining traces¶

Trace plots¶

Trace plots with ArviZ¶

Trace plots with bebi103¶

Interpetation of trace plots¶

Parallel coordinate plots¶

Parallel coordinate plots with ArviZ¶

Parallel coordinate plots with bebi103¶

Intepretation of parallel coordinate plots¶

Plots of marginalized distributions¶

Plotting marginalized distributions of one parameter¶

Plotting marginalized distributions with ArviZ¶

Plotting marginalized distributions with iqplot¶

Marginal posteriors of two parameters¶

Pair plots with ArviZ¶

Corner plots¶

Computing environment¶